What does System signifies-In Signals and Systems
- Usha Saha

- Sep 17, 2020
- 5 min read
Updated: Dec 28, 2024
The meaningful interconnection between a physical device and component is called a system. A #system can also be defined as an operator that maps the relationship between the input signal and the output signal by the process of transformation. The article overlays an absolute overview of the system and its classification.

Alike to #signal, the system can also be broadly classified into a continuous-time system and discrete-time system. In continuous-time, both the input and outputs are continuous-time signals whereas in a discrete-time system both the input and outputs are discrete-time signals. The example of a system is the electrical system, mechanical system, etc.

Classification of systems
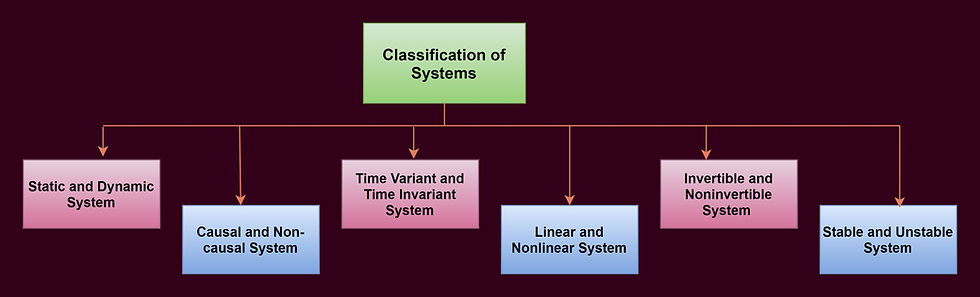
1) Static and Dynamic system
In a static system, the output at any instant of time depends only on the present value of the input. This signifies that the output does not depend on the past or future values of the input, therefore a static system is also called a system with no memory or energy storage elements. Let's understand the static system with the help of an example.
Example:- y(t)=2x(t)Note:- Here '2' is the coefficient, which does not affect the system.
for the above example substitute different values of t and check the system performance.
let us check for t= -1,0,1
for t=-1; y(-1)=2x(-1) ==> the output depends on the present value of input.
for t=0; y(0)=2x(0) ==> the output depends on the present value of input.
for t=1; y(1)=2x(1) ==> the output depends on the present value of input.
Hence the system is static.
In a dynamic system, the output at any instant of time depends on the past or future values of input. Therefore dynamic systems are called systems having memory. let's check for the dynamic system the same as we did for the static one.
Example:- y(t)= x(t)+x(t+1)+x(t-1).
For the above example to check if it is a static or dynamic system substitute different values of t.
let's check for t=0,1
for t=0; y(0)= x(0)+x(0+1)+x(0-1).
y(0)= x(0)[present value]+x(1)[future value]+x(-1)[past value]
Here for t=0; the output depends on future as well as past values of input with respect to zero which clearly indicates that the system is a dynamic system. Hence no need to check for other values.
2) Causal and Non-causal system.
The response of a casual system to input does not depend on future values of that input but depends only on the present or the past values of the input. Whereas if the response of the system to an input depends on the future value of that particular input then the system is a non-causal system. Let us understand the concept with the help of some examples.
Examples:-
y(t)= x(t) ==> casual system(check by substitution of different values of t ).
y(t)=x(t-1) ==> causal system.
y(t)=x(t+2) ==> non-causal system.
y(t)=x(t)+x(t+1)+x(t-1) ==> non-causal system.
Additional point:- The Anti-causal system is a system in which the output of the system depends only on the future values of input.
3) Time-variant and Time-invariant system.
This is a very essential type of classification of systems. A time-invariant system is one whose input-output relation do no vary with time, in other words, a time-invariant system is a system in which any time delay in the input must be reflected in the output. A system that does not follow this property is called a time-variant system.
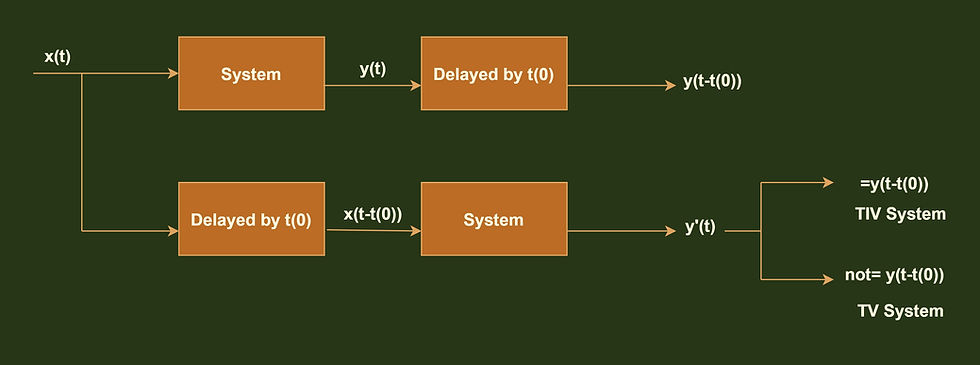
Let us understand the concept of Time-variant and Time-invariant system with some examples as some times it becomes complex to identify the system.
Sample:-
y(t)=x(2t)
to start with first identify the system,
here x(t) ---> system ---> after #scaling by a factor of 2 ---> x(2t) = y(t)
Delayed output
y(t) --> y[t-t(0)] = x[2(t- t(0))] y(t) is delayed by t(0)
y(t)= x(2t-2t(0))Delayed input
x(t) --> x(t- t(0)) =x(2t-t(0)) x(t) is delayed by t(0)
x(t)=x(2t-t(0))The input and output are no same after the #delay operation,hence the system is a Time-variant system.
y(t)= 2+ x(t)
here x(t) ---> system ---> after #shifting by a factor of 2 ---> 2+x(t) = y(t)
Delayed output
y(t) --> y[t-t(0)] = 2+x[(t- t(0))] y(t) is delayed by t(0)
y(t)= 2+x(t-t(0))Delayed input
x(t) --> x(t- t(0)) =2+x(t-t(0)) x(t) is delayed by t(0)
x(t)=2+x(t-t(0))The input and output are same after the delay operation,hence the system is a Time-invariant system.
Added information:- For a system to be a Time-invariant system.
There should not be any time scaling in the input or in the output.
Coefficients should be constant.
Any added or subtracted term in the system relation(other than the input and output ) must be constant or zero.
A split system is always a Time variant system.
4) Linear and Non-Linear system
The system which follows the principle of superposition is recognized as a #linear system, otherwise, the system is a #non-linear system. If a system is both time-invariant and linear then the system is called an LTI (Linear Time-Invariant) system, and an LTI system plays a very significant role in signals and systems.
The principle of superposition comprise of-
Law of Additivity:- Its states that if an input x1(t) produces an output y1(t), and another input x2(t) produces an output y2(t) then when both inputs acting on the system simultaneously produces an output y1(t)+y2(t).
Law of Homogeneity:- It states that if an input is scaled by some factor say 'k' then the output is also scaled by the same factor.
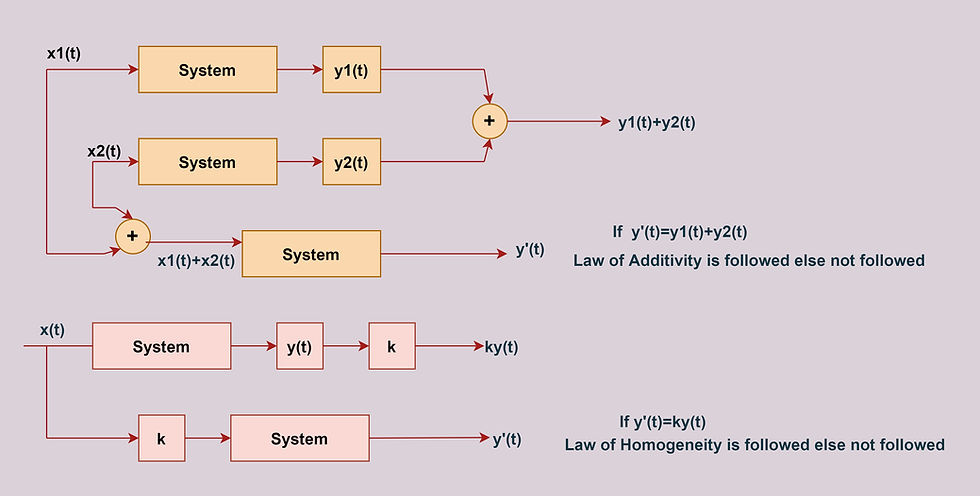
Points to Remember:-
System linearity is independent of the time scaling.
System linearity is independent of the coefficient used.
System linearity is dependent on the added/ subtracted term. This makes the system non-linear.
Both integral and differential operators are linear in nature.
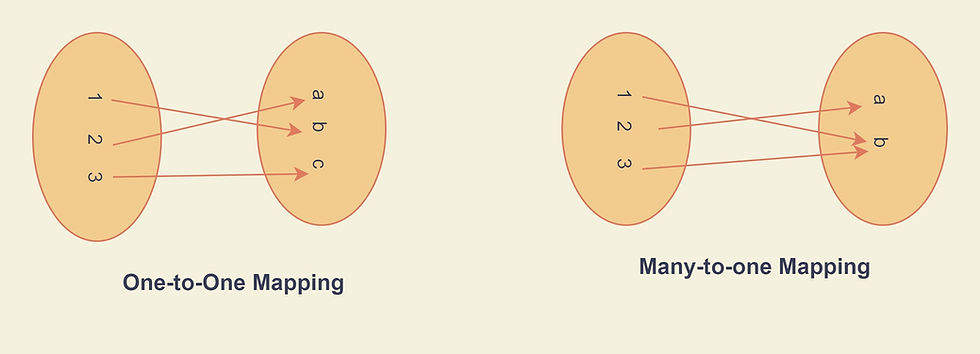
5) Invertible and Non-invertible system
In an invertible system, there is a one-to-one mapping between the input and output of the system at every instant of time. On the other hand in the case of the non-invertible system instead of one to one mapping there exists a many-to-one mapping.
6) Stable and Unstable system
A stable system follows the BIBO(Bounded Input Bounded Output) criteria. That is if bounded input results in a bounded output the system is said to be a stable system. On the other hand, an unstable system produces an unbounded output for a bounded input.
See Also
Order Electronics Projects
Want us to guide you through your project or make the project for you? Click on the button below or reach out to us via Call/WhatsApp at (+91) - 7600948607
You can -
Order Basic Electronics Projects
Order Embedded Systems Projects
Order IoT Projects
Order FPGA Projects
Order VLSI Projects
Order Image Processing Projects
Order Matlab Projects
Order TinkerCAD Projects
Order Proteus Projects
Click on the button below to fill out the project inquiry form -
Create Various Projects
Check out our Free Arduino Projects Playlist - Arduino Projects
Check out our Free Raspberry Pi Projects Playlist - Raspberry Pi Projects
Check out our Free TinkerCAD Projects Playlist - TinkerCAD Projects
Check out our Free IoT Projects Playlist - IoT Projects
Check out our Free Home Automation Projects Playlist - Home Automation Projects
Check out our Free NodeMCu Projects Playlist - NodeMCu Projects
Follow us -
Please do follow us i.e. #learnelectronicsindia to get daily updates about new blogs, videos, courses, products, offers, competitions, quizzes, and Internship Opportunities.






Hats off to Learn Electronics India for demystifying the concept of systems in signals and systems! The real-world applications discussed in the article make it much easier to grasp the significance of this topic. It's evident that the author not only knows their stuff but also has a talent for teaching complex ideas in a simple manner.
Brilliant explanation! Thanks, LearnElectronics India!