There are many logic gates and the #NAND gate is one of the gates that is commonly used in #digital circuitry.
But there is a property that makes the NAND gate stand out from the others. Yes, as the headline says, it is a universal gate; i.e. any logic gate or boolean expression can be made using NAND gates alone. Pretty cool stuff right!
A NAND gate is nothing but a gate that gives the inverse output of the #OR gate. Let us take a look at the truth table and symbolic representation.
Input A Input B Output Q
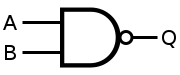
0 0 1
0 1 1
1 0 1
1 1 0
Let us now see how the implementation works.
NOT gate using NAND Gate
The NOT gate is a logical implementation that gives the reverse output of the input. This could be achieved by NAND Gate by simply joining the two inputs of the NAND Gate.
The expected output of the NOT gate is Q = NOT( A ).
The implementation of the OR gate using NAND gates is A NAND A.
AND gate using NAND gate
A NAND gate is an inverted circuit of an AND gate. So, to get an AND, we can simply reverse the NAND gate to get the desired output.
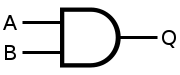
The desired AND output is as Q = A AND B.
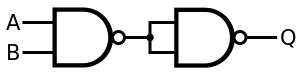
The implementation gives out the output as ( A NAND B ) NAND ( A NAND B ).
OR gate using NAND gate
The output of OR is true when at least one of the inputs is positive. To derive this, we can use #DeMorgan's law and can be characterized by output HIGH when one at least one of the inputs is HIGH.
The expected output of the OR gate is Q = A OR B.
The actual output of the OR gate using NAND is ( A NAND A ) NAND ( B NAND B ).
NOR gate using NAND gates
The NOR gate is obtained by inverting the output of the OR gate; i.e. neither of the inputs should be HIGH for the output HIGH.
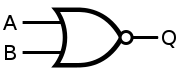
The expected output of the NOR gate is given by the expression Q = A NOR B.
The actual implementation of the NOR gate using NAND gate will be given using the expression [ ( A NAND A ) NAND ( B NAND B ) ] NAND [ ( A NAND A ) NAND ( B NAND B ) ].
XOR gate using NAND gates
There are mainly two ways to construct the XOR gate using NAND gates; one is using 4 gates, while the other involves the use of other5 gates.
The expected of the XOR gate is Q = A XOR B and the symbolic representation is given below.
Let us see the first implementation.
The XOR gate is designed by using the expression [ A NAND ( A NAND B ) ] NAND
[ B NAND ( A NAND B ) ].
The alternate implementation using 5 NAND gates is given below.
This implementation is derived by the idea that a NAND gate is an inverse logic of the OR gate and uses the expression [ B NAND ( A NAND A ) ] NAND [ A NAND ( B NAND B ) ].
XNOR gate using NAND gate
XNOR gate is a logic gate that gives the inverse output of an XOR gate. This can also be implemented in two ways.
The desired implementation is Q = A XNOR B and the symbolic representation is given below.
The first construction is done using NAND gates and constructed based on the expression
[ ( A NAND A ) NAND ( B NAND B ) ] NAND ( A NAND B ).
There is also another method of implementation using NAND gates and is done using the logic { [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ] } NAND { [ A NAND ( A NAND B ) ] NAND [ B NAND ( A NAND B ) ] }.
Now, we have seen the complete implementation of all the gates and have implemented them using NAND gates alone. Try out for yourself the magic of NAND as a universal gate by constructing boolean expression using these.